球のサイズと展開図の関係
布ボールや、何かしらの球体を作るにあたって、代表的な球体近似の展開図である舟型多円錐図法と正十二面体について、最終的なサイズ(直径)と組み立てる前のパーツのサイズの関係をまとめます。
一番最後に、球体のサイズ毎の型紙(基本図形が1つだけ描かれたもの)を用意しましたので、そちらもどうぞ。
舟型多円錐図法
舟型多円錐図法とは、舟の様な形を並べて球体を作る方法です。
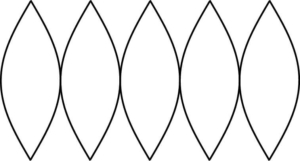
この舟の書き方はこんな感じ。式の導出は割愛します。
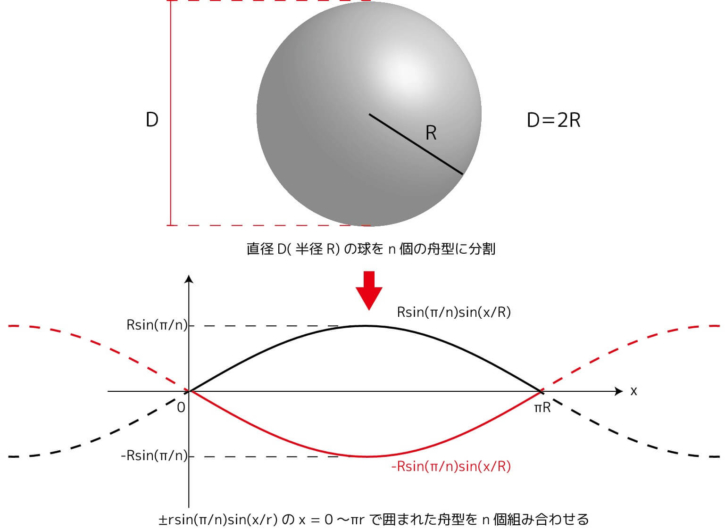
要はサインカーブを合わせたものです。曲線が適当だと組み立てた時にキレイになりません。
球体の半径と分割数で求まる舟の寸法はこんな感じです。単位はmmでもcmでもOK。
| 球体の直径:D | πR | n=4: Rsin(π/4) | n=6: Rsin(π/6) | n=8: Rsin(π/8) |
| 10 | 15.7 | 3.5 | 2.5 | 1.9 |
| 20 | 31.4 | 7.1 | 5.0 | 3.8 |
| 30 | 47.1 | 10.6 | 7.5 | 5.7 |
| 40 | 62.8 | 14.1 | 10.0 | 7.7 |
| 50 | 78.5 | 17.7 | 12.5 | 9.6 |
| 60 | 94.2 | 21.2 | 15.0 | 11.5 |
| 70 | 110.0 | 24.7 | 17.5 | 13.4 |
| 80 | 125.7 | 28.3 | 20.0 | 15.3 |
| 90 | 141.4 | 31.8 | 22.5 | 17.2 |
正十二面体
続いて、正十二面体。展開図の一例として以下の様なのがあります。
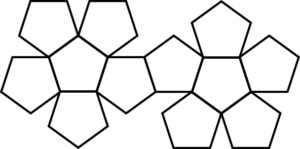
正十二面体の外接球の直径と、構成要素となる正五角形の外接円の半径及び一辺の長さの関係をまとめると、以下のようになります。
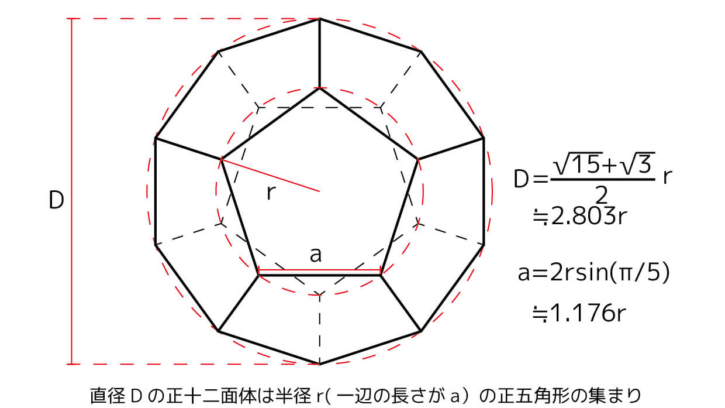
| 正十二面体の直径:D | 正五角形の一辺:a | 正五角形の半径:r |
| 10 | 4.2 | 3.6 |
| 20 | 8.4 | 7.1 |
| 30 | 12.6 | 10.7 |
| 40 | 16.8 | 14.3 |
| 50 | 21.0 | 17.8 |
| 60 | 25.2 | 21.4 |
| 70 | 29.4 | 25.0 |
| 80 | 33.6 | 28.5 |
| 90 | 37.8 | 32.1 |
型紙ダウンロード
球体のサイズ毎に、舟型多円錐図法と正十二面体の基本図形をA4に収まる範囲で描かれたものを用意しました。
サイズ(舟型の方は分割数も)を指定すると、それに見合った型紙がダウンロード出来ます。
2017.2.18追記 : 舟型多円錐図法を修正しました。






















